September 1, 2019 📊 Are pollsters herding their polls of the 2020 Democratic primary?
Plus, Joe Biden's declining favorability, and what if the DNC used different polls for its debate thresholds?
Welcome! I’m G. Elliott Morris, data journalist for The Economist and blogger of polls, elections, and political science. Happy Sunday! Here’s my weekly email with links to what I’ve been reading and writing that puts the news in context with public opinion polls, political science, other data (some “big,” some small) and looks briefly at the week ahead. Feedback? Drop me a line or just respond to this email.
Dear Reader,
This week’s main read: A prominent pollster admitted this week to re-doing polls so they match the conventional wisdom. That’s a huge infraction for public pollsters that could bias our averages in a major way (though maybe campaign pollsters don’t care). Are other pollsters herding, too?
Thanks for reading my weekly email. Please consider sharing online and/or forwarding to a friend. If you’d like to read more of my writing, I publish subscribers-only content 1-3x a week on this platform. Click the button below to subscribe for $5/month (or $50 annually). You also get the ability to leave comments on posts and join in on private threads, which are fun places for discussion!
My best!
—Elliott
This Week's Big Question
Are pollsters herding their 2020 Democratic primary polls?
Right now, the answer mostly depends on what you think the “true” distribution of polls should look like.

Image: Marco Bianchetti; Unsplash.com
A prominent pollster is biasing their results to match the conventional wisdom. The revelation comes after Monmouth University released what turned out to be a clear “outlier” poll of the 2020 Democratic primary last week: Joe Biden had lost 13 percentage points since the outlet’s last poll in June, their newest data indicated—a shocking decline. The problem? Monmouth’s poll had just 300 Democrats in it, and the number likely occurred from sampling error. But Patrick Murray, the director of the Monmouth University Polling Institute took a principled stance in arguing that even outlier data, which occur naturally with some non-zero frequency via way of statistical distributions, deserved to be released to the public. Outliers ensure that the mathematical properties of our aggregates remain in-tact.
Evidently, John Anzalone, of Anzalone-Liszt-Grove Research, disagreed. He tweeted:


Mr Anzalone’s comment that his firm throws numbers they “believe” are outliers in the “shit can” is a striking public admission of what pollsters and analysts call “herding”: the practice of either withholding estimates that look out of line or revising them altogether before publication. Herding is a huge problem because when pollsters suppress outlier data, the statistical properties of our averages change. We become too confident in a range of outcomes that is smaller than the one that actually exists (or would exist if pollsters released all the correct data). Some research says that polling averages can also become less accurate when pollsters herd their estimates.
Take this exercise as an example: Imagine you field ten surveys of the 2020 Democratic primary. Each one samples 500 registered voters. The ten polls come back as: 30%, 31, 33, 28, 20, 38, 33, 34, 29 and 27%. The standard error of those estimates is roughly 5 points and the average is 30. Mathematically speaking, that means that 95% of the time Joe Biden’s support in polls should come in between 30 and 20%. But what if the pollster who found Biden at 20% re-did his poll because it looked “off” and instead submitted a number that had Biden at 30? Then, the average rises just modestly to 31—not a large change, to be sure—but the standard error is slashed to 3 points. This is a huge deal. In the case of the smaller standard error, Biden’s support could hardly ever be as low as 20%. If we assume polls are distributed randomly, the biased data suggests that chance that Biden’s support is actually 20% is just 0.04%. This compares to a 5% chance for the raw one. Taking the numbers literally, this means that the pollster herding their data made an outcome with a 5% 125 times less likely just by releasing other data instead of the real ones. This overconfidence is the major danger of suppressing outliers.
This raises a question: are pollsters actually herding? The good news is that it doesn’t look like it. But the conclusions are a little tricker than that.
I took all of the polls of the 2020 Democratic primary that have been conducted by a live interviewer via the telephone and compared the standard error of the estimates to what we should “expect” to see for polls with similar sample sizes.
The following graph shows that there is not much difference between support for Joe Biden in actual polls and in 100,000 simulated “polls” with a mean of 30 and a sample size of 487 (which is the average n for phone polls over the past 4 months and corresponds to a standard error of about 4% when also accounting for non-sampling survey error). In fact, the random draw of fake polls with “mathematical” or “theoretical” standard errors (IE: derived from the sample size) match up so well with 100,000 simulations of polls with the actual standard error of 2020 polls that you can hardly make up the orange distribution under the purple one. (The green distribution shows the actual spread of polls today, whereas the orange one shows what that distribution would look like if firms released 99,976 more polls—a better benchmark for comparison that smooths over the bumps in the data.)
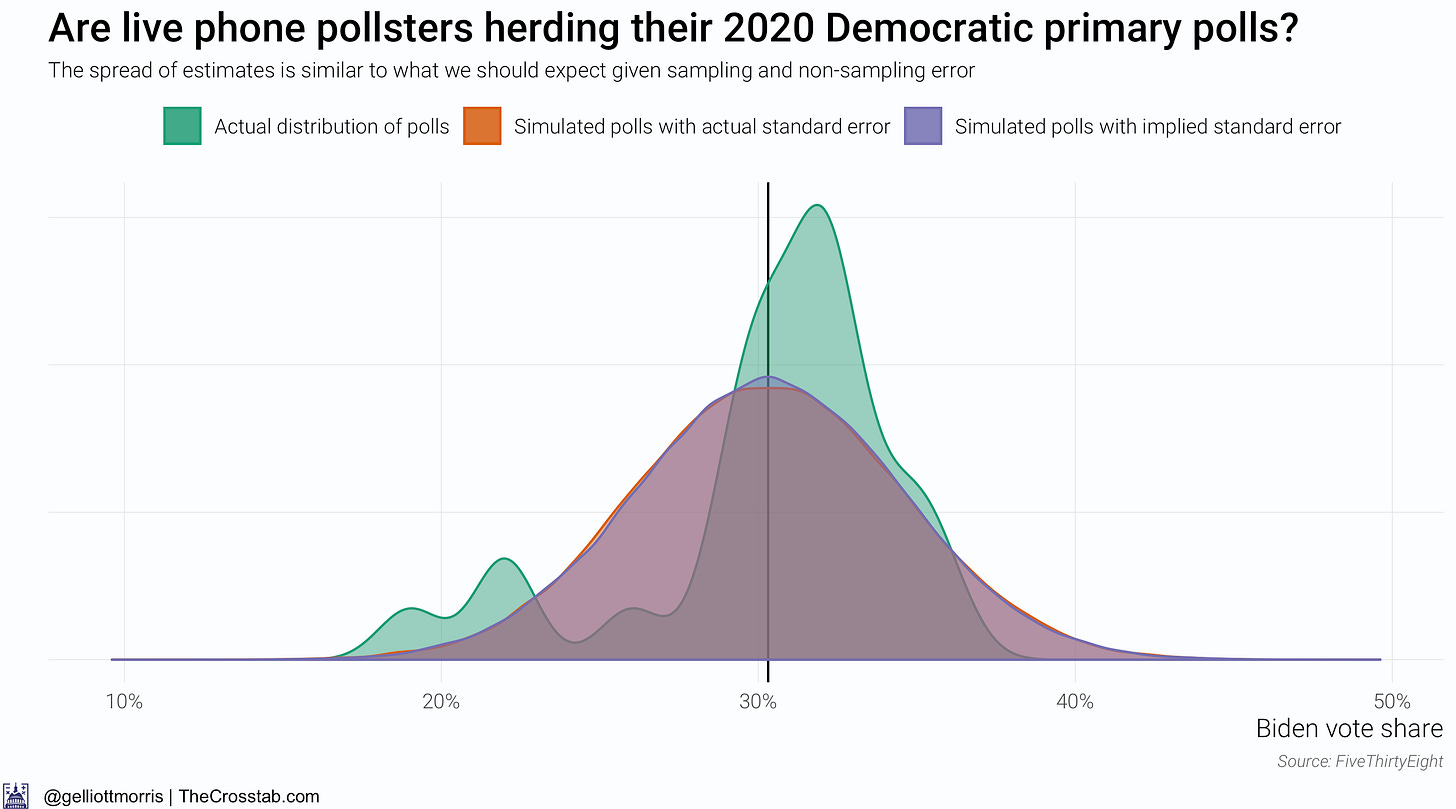
The above graph suggests that pollsters writ large are not herding because the distribution of Biden’s vote share in actual and hypothetical polls is not significantly different. However, this is not the only—or even ideal—way to look at the problem of herding.
Rather than looking at the distribution of the mean of Biden’s support (what the above graphs are effectively doing), we can explore the distribution of the standard error of today’s polls with the standard error of the hypothetical numbers. The graph below shows a distribution of possible standard errors of simulated and actual polls that I generated using a method called nonparametric bootstrapping, which computes the standard error of 100,000 samples of 10 actual polls and 100,000 samples of 10 simulated “polls” that have been generated based on the average sample size of a sample of ten real polls. Allow me to make that simpler:
Green curve: 100,000 times, pick ten polls and return the standard error of the “polls”
Orange curve: 100,000 times, pick ten polls, compute the average sample size, generate ten new “polls” based on that sample size, and return the standard error of the “polls”
This chart shows those distributions:
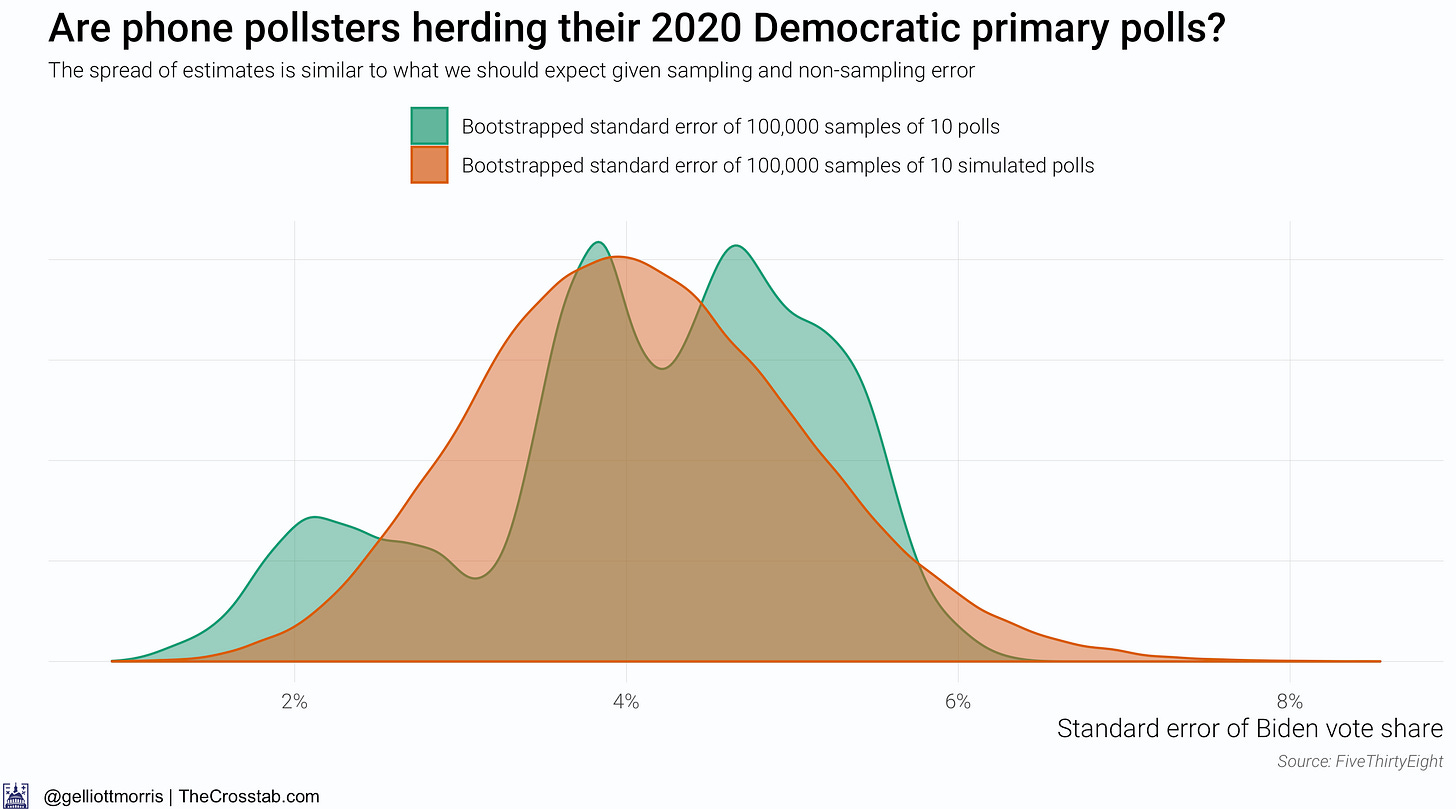
Although the distributions in the above graph *look* different, there is actually no statistically significant difference between their means (which is the mean of the actual vs hypothetical standard errors). (The odd shape of the green distribution is due mainly to the low n of our sample—there have only been 24 live-caller phone polls over the past 4 months).
So it doesn’t look like phone pollsters are herding their polls—but what about online pollsters? I’ve re-done the above analysis for pollsters who field their surveys online and show the results in the graphics below:
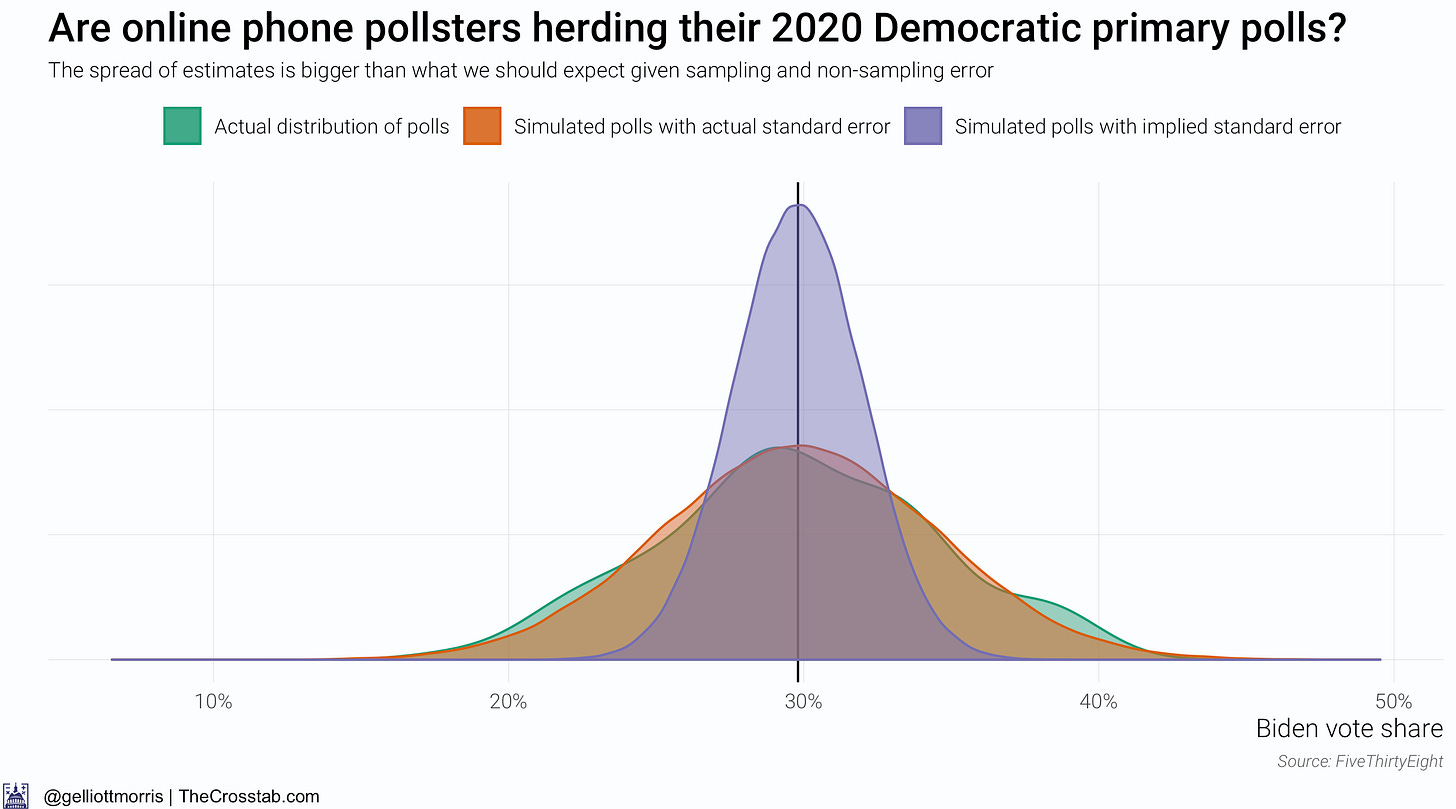
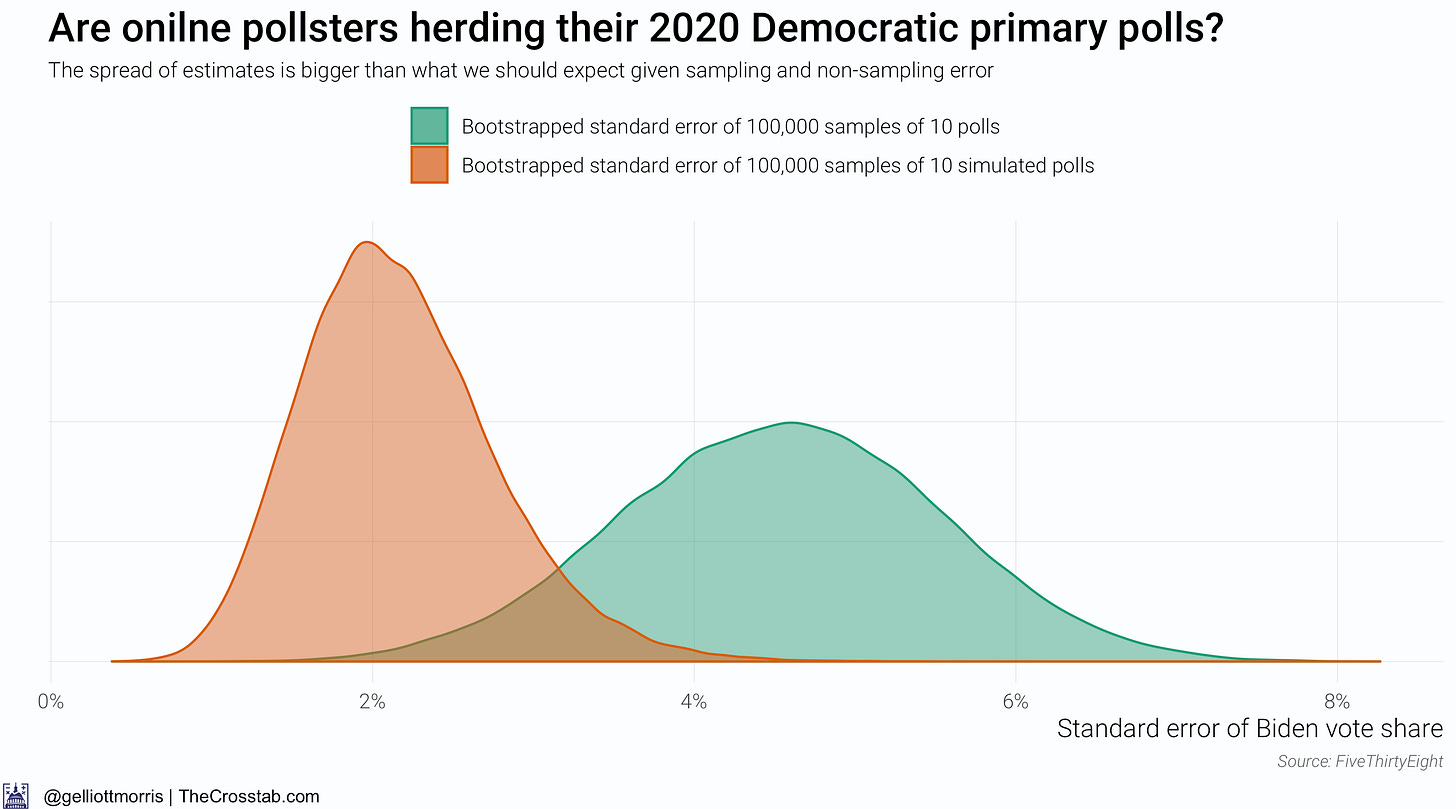
Weirdly, online polls are much more spread out than we would infer from their sample size alone. This is likely due to the fact that the two major online polling firms, Harris Interactive and YouGov, have been showing wildly different results for Biden (the formed generating good estimates for Biden and then latter not) and fielding a large number of surveys (or, at least larger than live phone pollsters.
What happens if we re-run the analysis only for polls from Harris Interactive (which is actually now called HarrisX)?
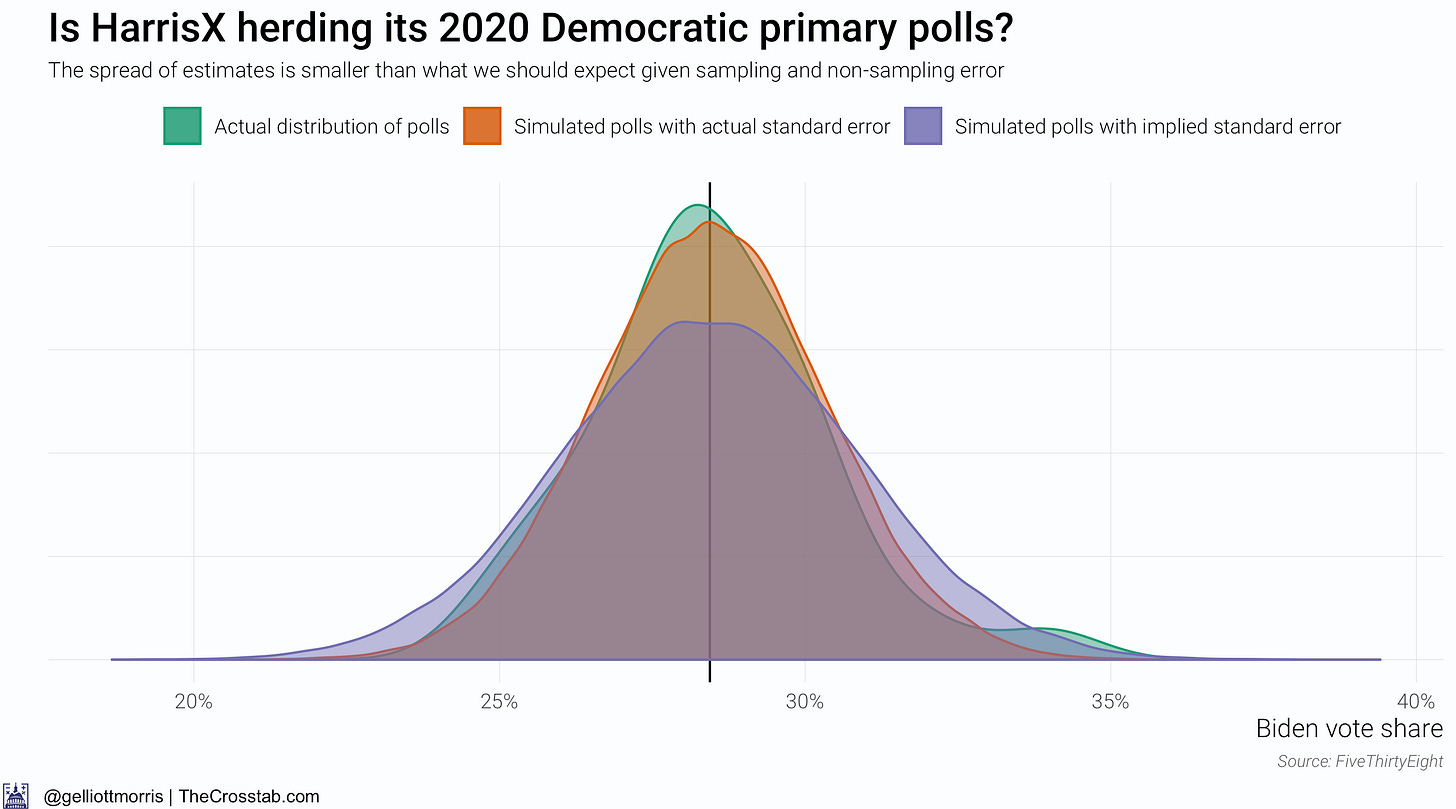
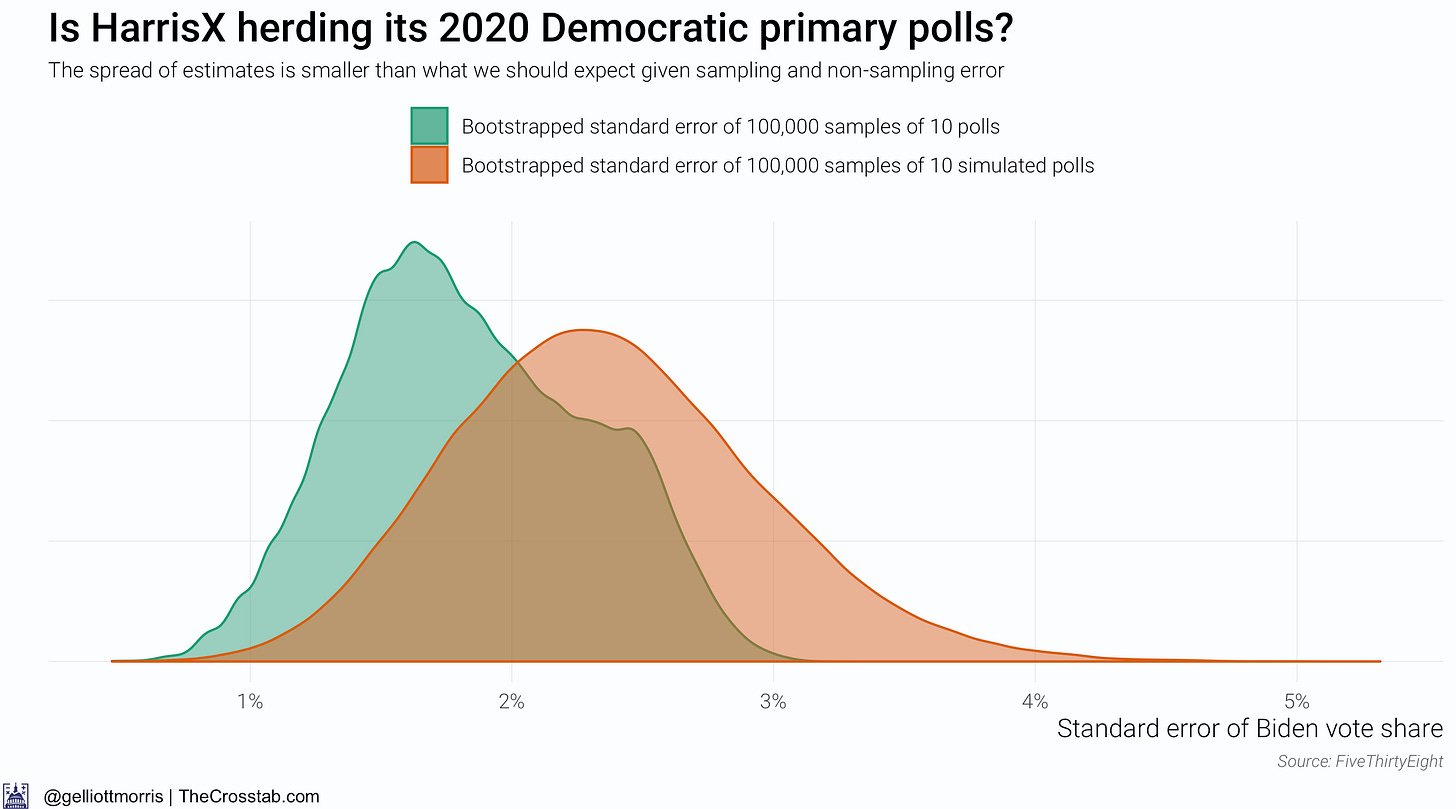
The above chart changes things—maybe. It above shows that the spread of HarrisX’s estimates for Biden’s vote share among registered Democratic voters is much smaller than what we should expect given sampling and non-sampling error (about 2x the sample size standard error). But this gives away a flaw with this research design: we don’t actually know what the spread of the simulated data should be. It might just be the error implied by a poll’s sample size, but Houshmand Shirani-Mehr, David Rothschild, Sharad Goel and Andrew Gelman reckon that the standard error for polls is roughly twice as large as the one that polling firms actually report—IE: twice as high as sampling error alone would imply. By the authors’ standards, one would infer that something is amiss with the HarrisX data. However, if you don’t believe their conclusions and factor in sampling error—the error implied by the poll’s sample size—alone, HarrisX’s polls are actually over-dispersed:
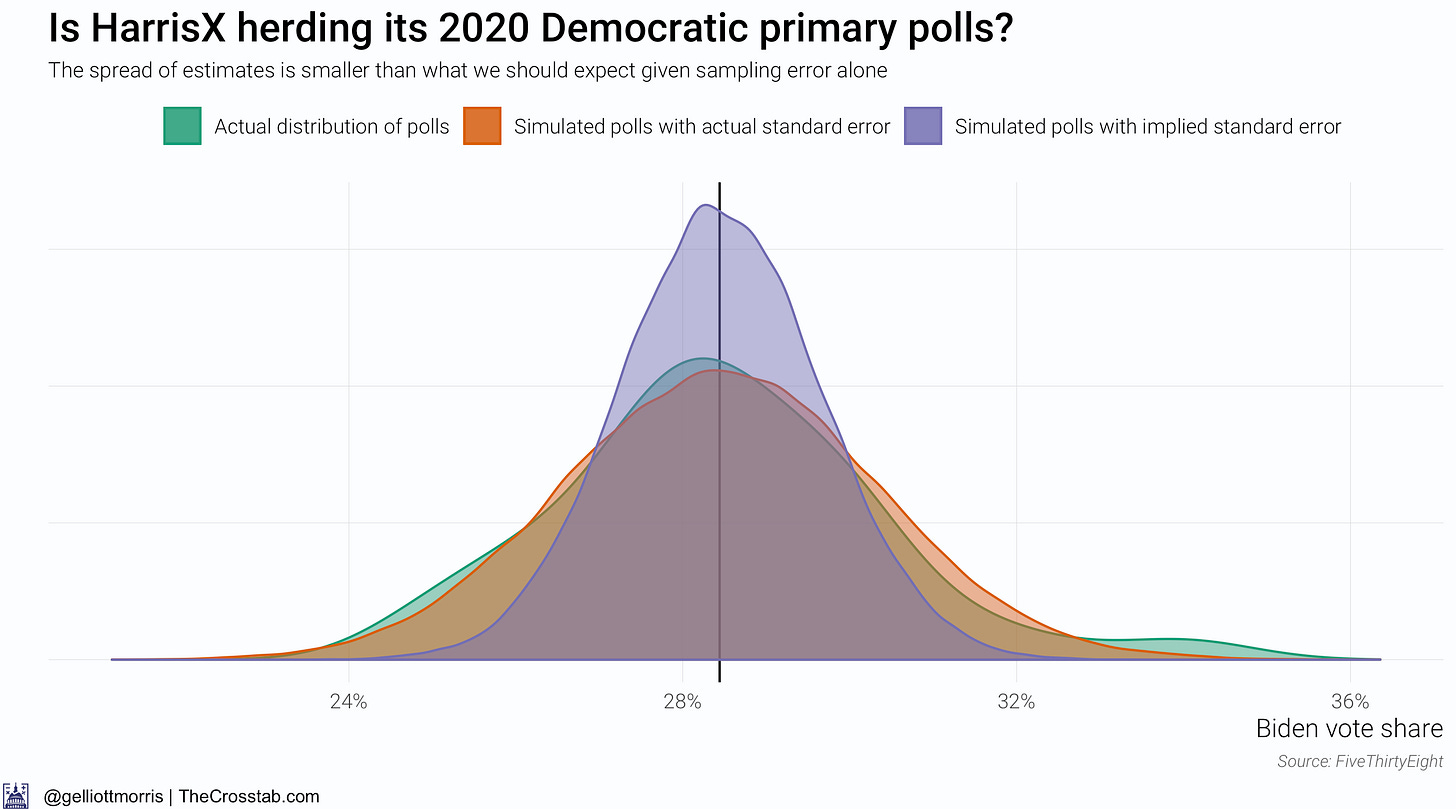
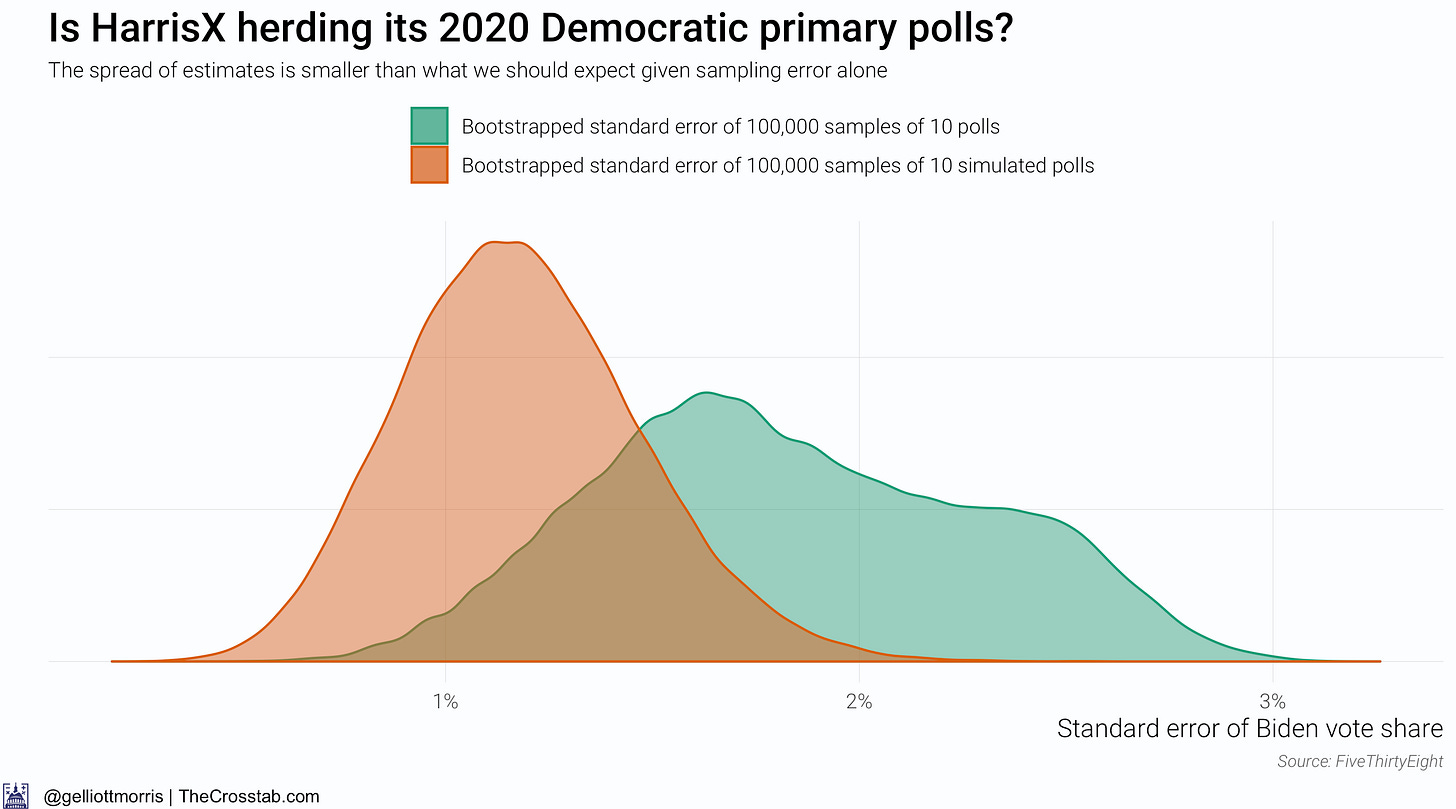
To be sure, I think the actual error is somewhere closer to twice as large as just sampling error, in line with the research from Shirani-Mehr et. al., than just sampling error alone.
…
The challenge of not knowing how spread-out polls ought to be makes it hard to identify which firms are herding. We also must reckon with the idea that we maybe be picking up false positives in the data. In that vein, it’s worth noting that YouGov’s numbers also have a smaller standard error than polls with the inferred amount of sampling and non-sampling bias would have. But since we can be relatively certain that YouGov is not herding its data, what use is a test that says it is?
In sum, it doesn’t look like pollsters writ large are herding. Or at least we can’t be sure with these methods.
But that doesn’t make John Anzalone’s admission any less severe.
And now, some of the stuff that I read (and wrote) over the last week.
Posts for subscribers:
August 29: Bad economic news could doom Trump. Polls say that the president has little else to lean on.
Political Data
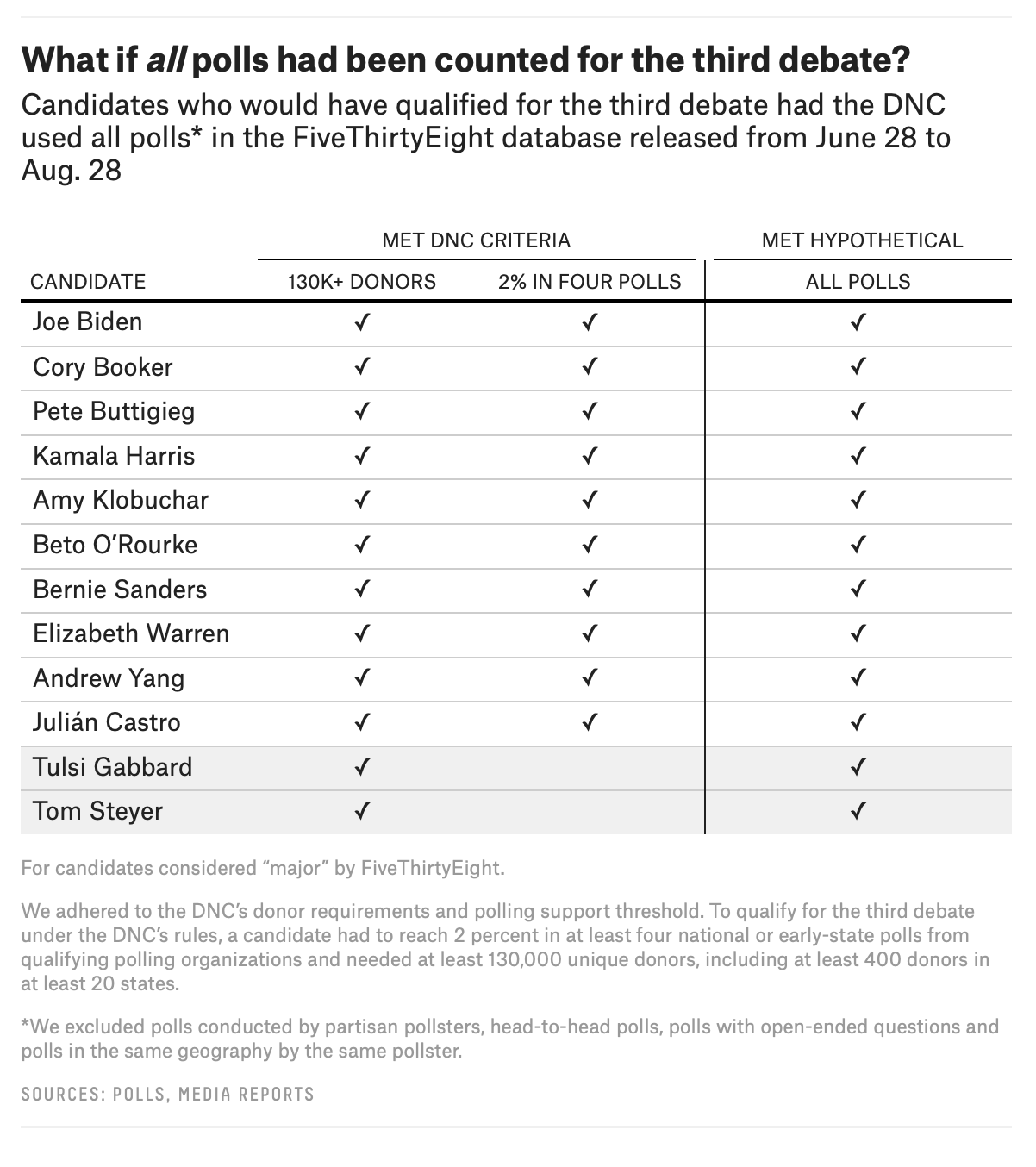
Geoffrey Skelley (538): “What If The Third Debate Were Based On Different Polls?”
What would the debate stage look like if the list or type of eligible polls were different? Gabbard, in particular, has taken the Democratic National Committee to task for the specific pollsters included in its list of approved polling organizations, arguing that had the list of pollsters been expanded, she would have had at least 2 percent support in more than 20 polls conducted during the third debate qualification window. And in fairness to her, understanding how the DNC determines its list of approved polling organizations can be confusing. Gabbard did hit 2 percent in YouGov’s latest national survey sponsored by The Economist, but it didn’t count toward qualifying for the debate.
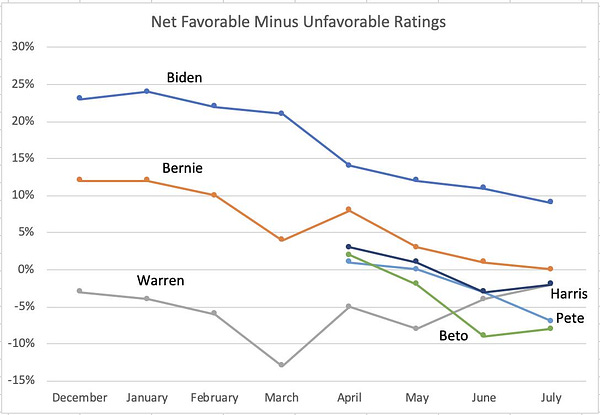
Matt Grossmann on Twitter: “Biden & Bernie have steadily lost net favorability this year. Less well-known candidates have also declined. Warren is a bit of an exception, starting low with some improvement. The declines are driven by Republicans & Independents.”

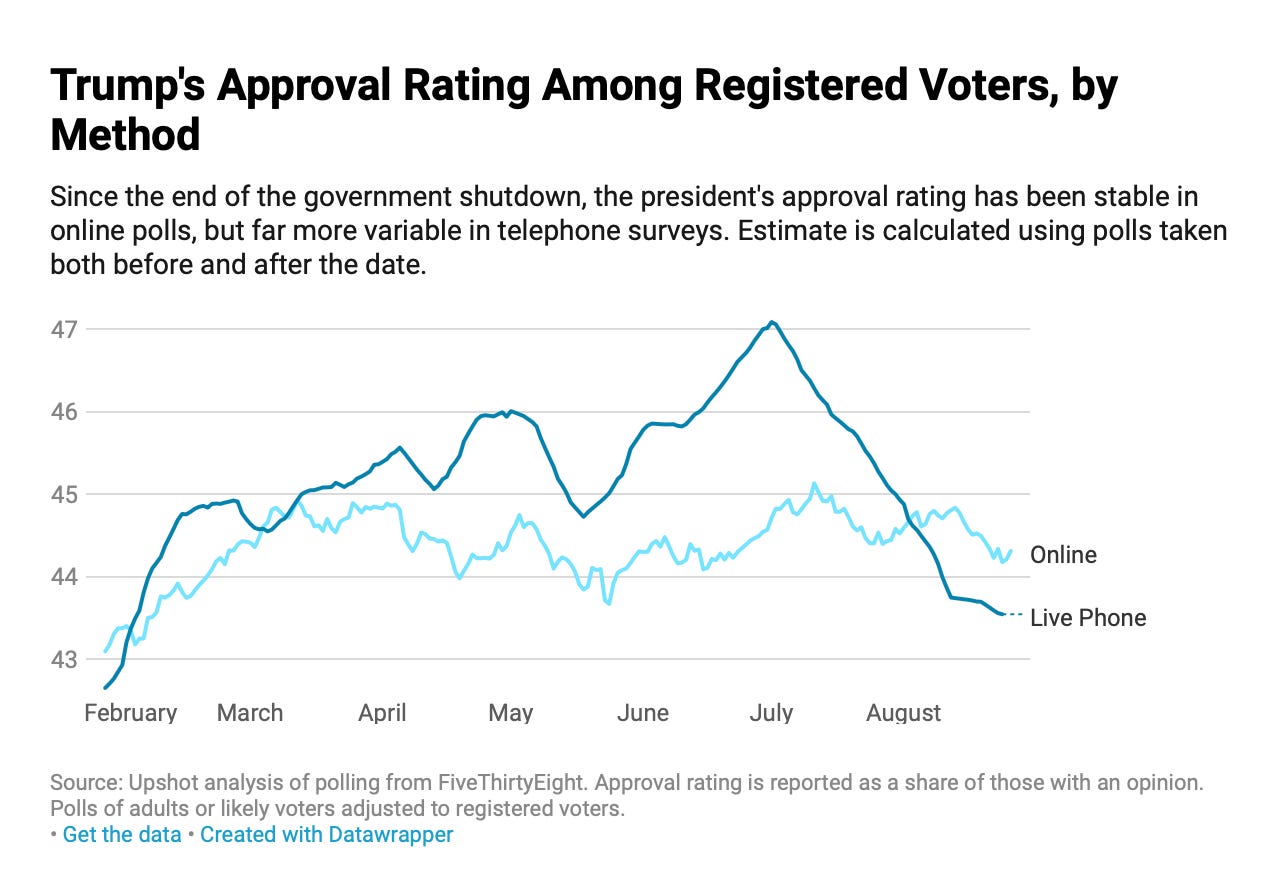
Nate Cohn (The Upshot): “Two Polling Methods, Two Views of Trump’s 2020 Re-election Chances”
But if Mr. Trump and this era are unique, then 2020 might hinge on turnout: In a polarized environment with few persuadable voters left, little else would matter. Democrats might not need to worry about whom they nominate, as long as they can energize irregular voters. In the extreme, you could argue that the president has basically already lost re-election: Voters have made up their minds, and too many dislike him for him to win.
These theories are impossible to test before the election. But the main evidence for the polarization theory comes from the polls. They have always shown the president’s approval ratings well under water, with around half of voters saying they strongly disapprove of his performance. If that ever stopped being true, it would essentially disprove the theory.
That’s why movement in the polls has been particularly interesting lately. Over the last few months, online polls and live-interview polls have split in a way that would either support or undermine each of these theories, depending on which set of polls you believe.
The online polls support the polarization story: They show that the president’s approval rating has been astonishingly steady throughout his presidency, including over the last month.
Other Data and Cool Stuff:
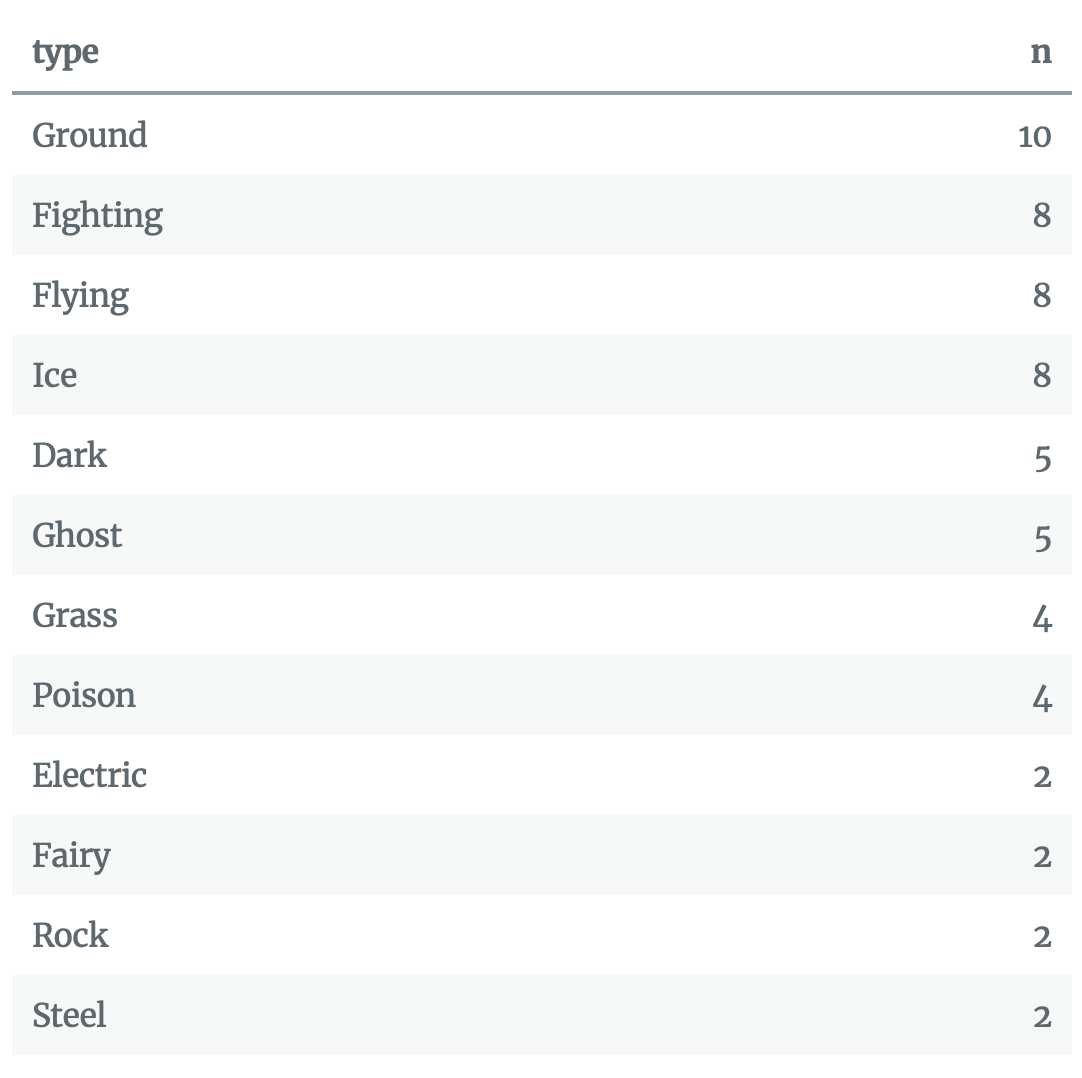
Emily Robinson: “What Types Should You Have on Your Pokémon Team?”
Political Science, Survey Research, and Other Nerdy Things
Slides from my presentation at #APSA2019: “Why forecast elections? And how (not) to do so”

What I'm Reading and Working On
I’ll be writing about America’s attitudes toward the economy and about hurricanes this week. I’m reading “The Power of Habit” by Charles Duhigg, which is full of fascinating stories about marketing, psychology and the biology of the human brain.
Something Fun
I thought this video from Kurzgesagt, a popular science-focused youtube channel, was quite entertaining, thought-provoking and well written.
Thanks for reading!
Thanks for reading. I’ll be back in your inbox next Sunday. In the meantime, follow me online or reach out via email. I’d love to hear from you!
If you want more content from me, I publish subscribers-only posts on Substack 1-3 times each week. Sign up today for $5/month (or $50/year) by clicking on the following button. Even if you don't want the extra posts, the funds go toward supporting the time spent writing this free, weekly letter. Your support makes this all possible!


